Howdy, Stranger!
It looks like you're new here. If you want to get involved, click one of these buttons!
Quick Links
Ring shapes using KLayout
Hi,
I am trying to create a ring shape in Layout. First I used the donut shape and exported it to cadence. Apparently the design gives me an error with the DRC check. The donut shape created using the Klayout does not snap/fit to the grid points. One example of a ring structure fitting the DRC regulations is attached here.
Can I create such structure using the KLayout?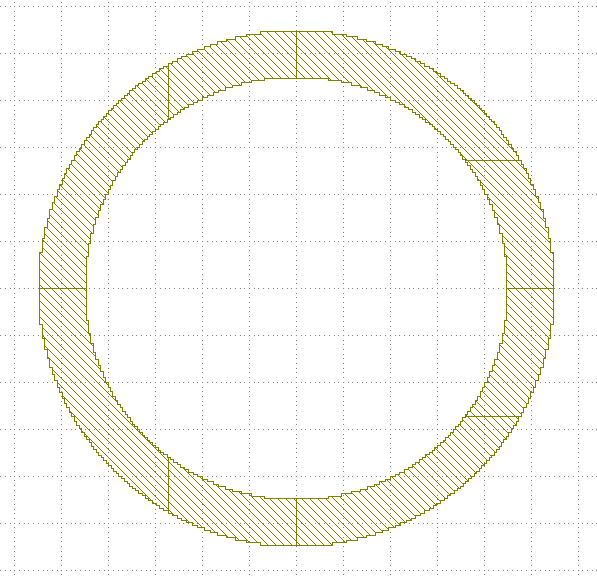
Comments
You can create such structure very easily with Klayout.
Create two boxes and apply "round corners". Then subtract one box to the other.
See the "Selection" menu.
Hi Rakesh,
I think the request is about creating the pixelized pattern.
There is no function readily available for this kind of transformation yet, but it can be coded. Here for example is a DRC script which turns a layer with all-angle polygons in to one with staircase approximation:
Matthias
Matthias, Thank you for the help. I am new to ruby and do not where to get start. All I new is to go to the macros and compile this code, but how does this effect the layout diagram is not something I can understand.
Can you please direct me towards some simple RUBY examples to begin with?
Hi Rakesh,
this is a DRC script. Go to the Macro editor, open the DRC tab, create a new DRC script and paste the above code.
If you run it, it will take input from layer 1, datatype 0, apply the steps and write it to layer 10, datatype 0 in your original layout. See the last lines for these details.
Regards,
Matthias